BAB I
PENDAHULUAN
1.1
Latar Belakang
Untuk menunjang bertambahnya permintaan
energi listrik harus diimbangi dengan peningkatan kualitas energi listrik yang
disalurkan. Dengan melakukan suatu analisa terhadap sistem tenaga merupakan
salah satu cara untuk meningkatkan kualitas energi listrik, dikarenakan analisa
sistem tenaga mencakup beberapa permasalahan utama dalam system tenaga yaitu
aliran beban, hubung singkat, stabilitas dan pengaman. Keempat masalah tersebut
adalah faktor penting untuk meningkatkan kualitas energi listrik yang
disalurkan.
Untuk menyelesaikan studi aliran daya
dengan metode iterasi (numerik) telah banyak dikembangkan dengan menggunakan
komputer digital. Bermacam metode penyelesaian studi aliran daya telah semakin
banyak dikembangkan sejalan dengan makin berkembangnya konfigurasi jaringan
system tenaga, baik dalam perencanaan, pengembangan, maupun pengoperasian.
Sampai saat ini beberapa metode yang sering dipelajari adalah Metode Gauss
Seidel, Metode Newton Rhapson, Metode Fast Decoupled dan Metode runge-kutta
orde 4 . Masing-masing metode untuk
analisa aliran daya mempunyai kekurangan dan kelebihan satu sama lain.
Dalam makalah ini penulis akan
membandingkan keandalan antara metode Gauss-Seidel, metode Newton Raphson, metode
Fast Decoupled dan metode runge-kutta orde 4 dalam menyelesaikan masalah aliran
daya untuk mengetahui kelebihan dan kekurangan masing-masing metode.
1.2
Tujuan
Tujuan dari
pembuatan makalah ini adalah untuk :
1. Untuk
mengetahui akan kelebihan dan kekurangan antara metode Gauss-Seidel, metode Newton Raphson, metode Fast Decoupled dan metode
runge-kutta orde 4 sehingga bisa
menentukan metode mana yang lebih baik dalam
penyelesaian
masalah analisa aliran daya.
2. Membuat suatu
perangkat lunak yang dapat membantu dalam menyelesaikan masalah perbandingan
metode Gauss-Seidel, metode Newton Raphson, metode Fast Decoupled dan metode runge-kutta agar mudah dalam
penganalisaan.
1.3
Rumusan Masalah
Rumusan masalah dari makalah ini adalah :
1. Bagaimanakah perbandingan
dari keempat metode tersebut?
2. Apa saja keuntungan dan
kelemahan dari ke empat metode tersebut?
BAB II
PEMBAHASAN
PENGGUNAAN
METODE GAUSS SEIDEL, METODE NEWTON RAPHSON, METODE FAST DECOUPLED DAN METODE
RUNGE-KUTTA DALAM STUDI ALIRAN DAYA
2.1 Metode
Gauss-Seidel
Aplikasi hasil bus ini adalah
Daya nyata dan reaktif pada bus i adalah
Di konjugatkan menjadi
mensubtitusikan
persamaan (3.2) dengan persamaan (3.1) hasilnya,
Dari hubungan diatas, hasilnya harus dipecahkan
oleh teknik iterasi. Persamaan (3.4) dipecahkan untuk Vi.
Persamaan aliran daya biasanya ditulis dalam
istilah elemen matrik admitansi bus.
Sejak itu elemen
diagonal-off pada matrik admitansi bus Ybus, ditunjukkan oleh persamaan diatas,
yaitu Yij =
-yij , dan elemen
diagonal adalah Yii= Σ yij , persamaan menjadi,
Untuk generator bus (bus P-V) dimana sch
Pi dan Vi adalah ditentukan, persamaan (3.7) ditentukan untuk (k
+1) Qi . Untuk mendapatkan
(k+1) Vi ditentukan dengan menggunakan
persamaan,
dimana ei(k
+1) dan fi (k+1)
adalah komponen real dan imajiner tegangan (k +1)
Vi pada iterasi berikutnya.
Kecepatan konvergensi dapatm ditambahkan oleh aplikasi factor ketelitian pada iterasi
berikutnya yaitu
dimana
α = faktor
kecepatan.
Vcal = Tegangan yang
dihitung (calculated)
Iterasi dilanjutkan sampai magnitude elemen
dalam kolom ΔP dan ΔQ adalah lebih
kecil dari nilai spesifik. Tipe daya tak sebanding ketelitiannya adalah 0.001
pu. Ketika solusi konvergen, daya aktif dan reaktif pada slack bus dihitung.
2.2 Metode
Newton Raphson
Dasar dari metode Newton Raphson dalam
penyelesaian aliran daya adalah deret Taylor untuk suatu fungsi dengan dua
variable lebih. Metode Newton Rhapson menyelesaikan masalah aliran daya dengan
menggunakan suatu set persamaan non linier untuk menghitung besarnya tegangan
dan sudut fasa tegangan tiap bus.
Daya injeksi pada bus i
adalah :
Dalam hal ini dilakukan pemisahan daya nyata
dan daya reaktif pada bus i. Pemisahan ini akan menghasilkan suatu set
persamaan simultan non linear.
Dalam koordinat kutub
diketahui :
Karena e (δj- δi+θij)= cos (δj- δi+θij) + j sin (δj-
δi+θij), maka pemisahan daya pada bus i
menjadi komponen real dan imajiner adalah :
Nilai Pi dan Qi telah diketahui, tetapi
nilai Vi dan
δi
tidak diketahui kecuali pada slack bus. Kedua persamaan non linier tersebut
dapat diuraikan menjadi suatu set persamaan simultan linier dengan cara
menyatakan hubungan antara perubahan daya nyata ΔPi dan daya reaktif ΔQi terhadap
perubahan magnitude tegangan ΔVi
dan sudut fasa tegangan Δδi.
Elemen – elemen matriks Jacobi dapat
dihitung dengan menggunakan persamaanpersamaan daya nyata dan reaktif pada bus
I dari persamaan (3.14) dan (3.15) yang diturunkan sebagai berikut : (i = 1, 2,
… , n-1)
Elemen-elemen
off-diagonal dari J1 adalah :
Elemen diagonal dari J1 adalah :
Elemen off-diagonal dari J2
adalah :
Elemen diagonal dari J2 adalah :
Elemen off-diagonal dari J3 adalah
:
Elemen diagonal dari J3 adalah :
Elemen-elemen off-diagonal dari
J4 adalah :
Elemen diagonal dari J4 adalah :
Elemen-elemen matriks Jacobi dihitung setiap
akan melakukan iterasi. Perhitungan iterasi dimulai dengan memberikan perkiraan
magnitude tegangan dan sudut fasa tegangan mula-mula. Perubahanperubahan dalam
daya nyata dan daya reaktif yang telah dijadwalkan dikurangi dengan daya nyata
dan daya reaktif yang dihitung dari persamaan (3.17) sampai (3.24)
ΔPik = Pi(terjadwal) – Pik ΔQi
k = Qi(terjadwal) – Qik i = 1, 2, … , n-1 (3.25)
Elemen-elemen
matriks Jacobim dihitung dengan menggunakan magnitude tegangan dan sudut fasa
tegangan estimasi mula-mula. Dengan menggunakan metode invers langsung maka
persamaan linier (3.16) dapat dipecahkan untuk mendapatkan nilai-nilai magnitude
tegangan dan sudut fasa tegangan estimasi yang baru pada tiap bus (kecuali
slack bus), sebagai berikut :
Proses iterasi kembali lagi ke proses awal
dan hal ini terus diulangi sampai ΔPik dan ΔQi
k untuk semua bus (selain slack bus) memenuhi harga toleransi yang diberikan
(biasanya diambil ≤ 0.001).
Δi k+1 = δik
+ Δ δik
|Vi |k+1 = |Vi |k + Δ |Vi
|k
(3.26)
Jadi iterasi selesai bila,
Δ
δik
≤ 0.001
Δ
|Vi
|k ≤ 0.001
2.3 Metode Fast Decoupled
Karakteristik yang menarik dari
pengoperasian sistem tenaga dalam kondisi tunak adalah ketergantungan antara
daya nyata dengan sudut fasa tegangan bus dan antara daya reaktif dengan
magnitude tegangan bus. Dalam kondisi ini, danya perubahan yang kecil pada
magnitude tegangan tidak akan menyebabkan perubahan yang berarti pada daya
nyata.
Sedangkan perubahan kecil pada sudut
tegangan fasa tidak akan menyebabkan perubahan berarti pada daya reaktif.
Ini dapat dibuktikan pada
pendekatanpendekatan dilakukan untuk menyatakan keterkaitan
antara P dan δ serta antara Q dan V.
Dengan menggunakan bentuk koordinat kutub
maka solusi permasalahan diperoleh yaitu dengan cara mengasumsikan
elemen-elemen sub matriks J2 dan J3 dalam matriks Jacobi adalah nol.
dipersamaan
diatas dapat dilihat bahwa apabila pada pembentukan daya aktif faktor yang
menentukan adalah sudut tegangan jadi adanya perubahan pada magnitude tegangan
tidak mempengaruhi daya aktif. Kondisi sebaliknya diperuntukkan pada persamaan
pembentukan daya reaktif yaitu perubahan kecil pada sudut fasa tidak akan
menyebabkan perubahan yang berarti pada daya reaktif.
Elemen-elemen matriks Jacobi yang diturunkan
dari persamaan (2.17) sampai (2.24) adalah :
Untuk J1 :
dimana,
Bij = Yij sin θij
Bii = Yii sin θii
Dapat dilihat
dari persamaan (2.15)
Untuk J2 :
Nij ≈ 0
Nii ≈ 0
Untuk J3 :
Jij ≈ 0
Jii ≈ 0
Untuk J4 :
dimana,
Bij = Yij sin θij
Bii = Yii sin θii
dilihat dari
persamaan (2.15)
Dalam bentuk
matriks, lambang elemen matriks
Jacobi dikoreksi
menjadi:
atau dalam format iterasi dapat
kita tulis :
Metode Decoupled ini mempunyai konvergensi
yang sama dengan metode Newton Rhapson. Keuntungan yang dimiliki oleh metode
ini adalah penggunaan memori komputer yang lebih kecil karena mengabaikan sub
matriks N dan J (atau J2 dan J3).
2.4
Metode Runge-Kutta orde 4
Metode Runge-Kutta dikembangkan untuk
menghindari penghitungan turunan-turunan yang berorde lebih tinggi. Sebagai
ganti dari turunan-turunan ini maka digunakan nilai-nilai tambahan dari fungsi
(f x,y )Kesederhanaanya telah membuat metoda ini menjadi sangat populer. Dengan
Penyelesaian Runge-Kutta Orde 4, dimana untuk menentukan harga x(t), tentukan
terlebih dahulu empat konstanta dalam bentuk persamaan (1) s/d (4) berikut
Sehingga algoritma perhitungan untuk harga x
berturut-turut dapat dicari dengan persamaan berikut
Untuk menentukan penyelesaian persamaan
ayunan dimana daya masukan P m diasumsikan konstan, pada operasi keadaan mantap
dimana P e = P m dan sudut daya mula-mula dinyatakan dalam bentuk persamaan (6)
berikut
dan
X1 adalah reaktansi transfer sebelum gangguan. Rotor berputar pada kecepatan
sinkron dan kemudian kecepatan putar berubah menjadi nol, sehingga diperoleh
persamaan (8) berikut
Gangguan tiga fasa terjadi salah satu
pertengahan saluran sehingga persamaan sudut daya dinyatakan dalam bentuk
persamaan (9) berikut
dan
X2 adalah reaktansi transfer selama gangguan. Dengan demikian persamaan ayunan
dinyatakan dalam bentuk persamaan (10) berikut
Persamaan (10) ditransformasikan kedalam
bentuk persamaan (11) dan (12) berikut
Untuk menentukan harga δ dan ω dengan
penyelesaian metoda Runge-Kutta orde 4, terlebih dahulu tentukan
harga-harga K1, K2
Selanjutnya harga δ dan ω dapat ditentukan
dengan menggunakan persamaan (21) dan (22) berikut
BAB III
PENUTUP
3.1 Kesimpulan
1.
Jumlah
iterasi untuk mencapai konvergen, metode Gauss-Seidel (29 Iterasi untuk
jaringan 5 Bus 7 Saluran) lebih banyak dibandingkan metode Newton Raphson (3
Iterasi untuk jaringan 5 Bus 7 Saluran) dan metode Fast Decoupled (8 Iterasi
untuk jaringan 5 Bus 7 Saluran). Ini membuktikan bahwa metode Newton Raphson
dan metode Fast Decoupled mempunyai kurva iterasi yang lebih baik daripada
metode Gauss Seidel.
2.
Untuk
masalah rugi-rugi daya saluran pada keempat metode hasilnya hamper mendekati
sama berarti ketelitian untuk perhitungan rugi-rugi daya hampir sama
ketelitiannya.
3.
Operasi
matematik metode Newton Raphson dan Fast Decoupled lebih sulit bila
dibandingkan dengan metode Gauss-Seidel dikarenakan metode Newton Raphson dan
Fast Decouple ada pembentukan matrik Jacobian, begitu pula dengan penyusunan
program komputernya, secara relative metode Newton Raphson dan FastDecoupled
memerlukan waktu lebih lama.
4.
Metode
Newton Raphson lebih sesuai untuk menghitung aliran beban pada sistem dengan
jumlah yang besar, dan kurang sesuai untuk sistem kecil, sedang metode
Gauss-Seidel bersifat sebaliknya.
5.
Jadi metode yang paling baik adalah metode
Fast Decoupled dikarenakan metode ini telah banyak penyempurnaan dari
metode-metode sebelumnya dan metode ini dapat diterapkan pada jaringan sistem
besar maupun kecil dan cepat mencapai
konvergen.
6.
Metode Runge-Kutta dikembangkan
untuk menghindari penghitungan turunan-turunan yang berorde lebih tinggi.
Sebagai ganti dari turunan-turunan ini maka digunakan nilai-nilai tambahan dari
fungsi (f x,y )Kesederhanaanya telah membuat metoda ini menjadi sangat populer.
Dengan Penyelesaian Runge-Kutta Orde 4, dimana untuk menentukan harga x(t)
3.2. Saran
1.
Penulis
menyarankan adanya pengembangan selanjutnya dari Makalah ini untuk dibandingkan
metodenya dengan metode-metode lainnya sebagai perbandingan. Dan juga dapat
dicoba diterapkan pada model sistem jaringan bus yang besar,contohnya seperti
model jaringan standar IEEE 57 bus 80 saluran.
2.
Simulasi
dalam Makalah ini masih menggunakan asumsi umum studi aliran daya, yakni
kondisi system dianggap stabil (Balance System) untuk itu penulis
menyarankan untuk mencoba menggunakan pula pada kondisi tak stabil (Unbalanced System)
DAFTAR PUSTAKA
1.
A.
Arismunandar, DR, S. Kuwahara, DR, “Teknik Tenaga Listrik Jilid II”,
PT Pradnya Paramita, Jakarta, 1993.
2.
Abdul Kadir, “Dasar Pemrograman Delhpi 5.0 Jilid
1”, Penerbit Andi, Yogyakarta, 2001.
3.
Abdul Kadir, “Dasar Pemrograman Delhpi 5.0 Jilid
2”, Penerbit Andi, Yogyakarta, 2001.
4.
Antony Pranata, “PemrogramanBorland Delphi Edisi
2”, Penerbit Andi, Yogyakarta, 1998.
5.
Budiono
Mismail, “Analisa Sistem Tenaga”, Lembaga Penerbitan Universitas
Brawijaya, Malang, 1983.
6.
Basu, Pranamita & Aiswarya Harichandan, Power
System Stability Studies Using Matlab, National Institute of Technology
Rourkela, (2008)
7.
Ulum, Misbahul, Studi
Stabilitas Transient Tenaga Listrik dengan Metode Kriteria Luas Sama
Menggunakan Matlab, Universitas Negeri Surabaya, (2007).
8.
Irrine Budi Sulistiawati, Muhammad Abdillah,
Adi Soeprijanto, Prediksi Waktu Kritis Pemutusan Sistem Kelistrikkan Jawa –
Bali 500 KV Dengan Menggunakan Metoda Runge – Kutta Orde 4, Procedding,
Seminar Sistem Tenaga Listrik, Institute Teknologi Sepuluh November (ITS),
(2006)


.png)
.png)









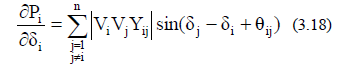
.png)
.png)
.png)
%2B-%2BCopy.png)





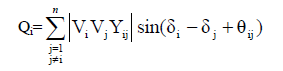


.png)
.png)


.png)



great.. thank you so much.
BalasHapus